Unidad 3 Redes (2) by on Scribd
Aplicación De Matemáticas Discretas
viernes, 21 de junio de 2019
martes, 11 de junio de 2019
problema agente viajero
En el Problema del Agente Viajero - TSP (Travelling Salesman Problem), el objetivo es encontrar un recorrido completo que conecte todos los nodos de una red, visitándolos tan solo una vez y volviendo al punto de partida, y que además minimice la distancia total de la ruta, o el tiempo total del recorrido.
Este tipo de problemas tiene gran aplicación en el ámbito de la logística y distribución, así como en la programación de curvas de producción.
El problema del agente viajero tiene una variación importante, y esta depende de que las distancias entre un nodo y otro sean simétricas o no, es decir, que la distancia entre A y B sea igual a la distancia entre B y A, puesto que en la práctica es muy poco probable que así sea.
La cantidad de rutas posibles en una red está determinada por la ecuación:
(n-1)!
Es decir que en una red de 5 nodos la cantidad de rutas probables es igual a (5-1)! = 24, y a medida que el número de nodos aumente la cantidad de rutas posibles crece factorialmente. En el caso de que el problema sea simétrico la cantidad de rutas posibles se reduce a la mitad, es decir:
( (n-1)! ) / 2
Lo cual significa un ahorro significativo en el tiempo de procesamiento de rutas de gran tamaño.
MÉTODOS DE SOLUCIÓN
La complejidad del cálculo del problema del agente viajero ha despertado múltiples iniciativas por mejorar la eficiencia en el cálculo de rutas. El método más básico es el conocido con el nombre de fuerza bruta, que consiste en el cálculo de todos los posibles recorridos, lo cual se hace extremadamente ineficiente y casi que se imposibilita en redes de gran tamaño. También existen heurísticos que se han desarrollado por la complejidad en el cálculo de soluciones óptimas en redes robustas, es por ello que existen métodos como el vecino más cercano, la inserción más barata y el doble sentido. Por último se encuentran los algoritmos que proporcionan soluciones óptimas, como el método de branch and bound (ramificación y poda), que trabaja el problema como un algoritmo de asignación y lo resuelve por medio del método simplex.
METODO DEL VECINO MAS CERCANO
El método del vecino más cercano es un algoritmo heurístico diseñado para solucionar el problema del agente viajero, no asegura una solución óptima, sin embargo suele proporcionar buenas soluciones, y tiene un tiempo de cálculo muy eficiente. El método de desarrollo es muy similar al utilizado para resolver problemas de árbol de expansión mínima.

El método consiste en una vez establecido el nodo de partida, evaluar y seleccionar su vecino más cercano. En este caso:

En la siguiente iteración habrá que considerar los vecinos más cercanos al nodo C (se excluye A por ser el nodo de origen):

En la siguiente iteración los vecinos más cercanos de D serán C, con quien ya tiene conexión, A quién es el nodo de origen y B, por esta razón B se debe seleccionar por descarte. Al estar en B todos los nodos se encuentran visitados, por lo que corresponde a cerrar la red uniendo el nodo B con el nodo A, así entonces la ruta solución por medio del vecino más próximo sería A, C, D, B, A = 7, 4, 15, 9 = 35 km.
Este es un caso en el que a pesar de tener una red compuesta por pocos nodos, el método del vecino más cercano no proporciona la solución óptima, la cual calculamos con el método de fuerza bruta como 31 km.
viernes, 7 de junio de 2019
torres hanoi
Las Torres de Hanói es un rompecabezas o juego matemático inventado en 1883 por el matemático francés Édouard Lucas.1 Este juego de mesa individual consiste en un número de discos perforados de radio creciente que se apilan insertándose en uno de los tres postes fijados a un tablero. El objetivo del juego es trasladar la pila a otro de los postes siguiendo ciertas reglas,como que no se puede colocar un disco mas grande encima de un disco mas pequeño. El problema es muy conocido en la ciencia de la computación y aparece en muchos libros de texto como introducción a la teoría de algoritmos.
La fórmula para encontrar el número de movimientos necesarios para transferir n discos desde un poste a otro es: 2n - 1
El juego, en su forma más tradicional, consiste en tres postes verticales. En uno de los postes se apila un número indeterminado de discos perforados por su centro (elaborados de madera), que determinará la complejidad de la solución. Por regla general se consideran siete discos. Los discos se apilan sobre uno de los postes en tamaño decreciente de abajo a arriba. No hay dos discos iguales, y todos ellos están apilados de mayor a menor radio -desde la base del poste hacia arriba- en uno de los postes, quedando los otros dos postes vacíos. El juego consiste en pasar todos los discos desde el poste ocupado (es decir, el que posee la torre) a uno de los otros postes vacíos. Para realizar este objetivo, es necesario seguir tres simples reglas:
- Solo se puede mover un disco cada vez y para mover otro los demás tienen que estar en postes.
- Un disco de mayor tamaño no puede estar sobre uno más pequeño que él mismo.
- Solo se puede desplazar el disco que se encuentre arriba en cada poste.
Existen diversas formas de llegar a la solución final, todas ellas siguiendo estrategias diversas.
tecnicas de conteo
TÉCNICAS DE CONTEO
- Diagrama de árbol
- Permutaciones
- Entran todos los elementos.
- Si importa el orden.
- No se repitan los elementos.
Si el ejercicio que se plantea sigue estas tres reglas la formula es aplicar Pn=n!
- Variaciones
- Combinaciones
Ejercicios Permutaciones
- ¿Cuantos números de 3 cifras diferentes se puede formar con los dígitos 1,2,3?
3*2*1=6 1,2,3
1,3,2
2,3,1
2,1,3
3,1,2
3,2,1
2.¿Cuantos grupos diferentes de tres vocales se puede formar sin que se repitan los elementos, usando 3 vocales: A,E,O?
3*2*1=6 A,E,O
A,O,E
E,A,O
E,O,A
O,A,E
O,E,A
3.¿Cuantos grupos de 4 elementos se puede formar con los digitos 3,5,7,9?
P4=4! 4*3*2*1=24
3,5,7,9 5,3,7,9 7,5,9,3 9,3,5,7
3,5,9,7 5,3,9,7 7,5,3,9 9,3,7,5
3,9,7,5 5,9,3,7 7,3,5,9 9,7,3,5
3,9,5,7 5,9,7,3 7,3,9,5 9,7,5,3
3,7,9,5 5,7,3,9 7,9,3,5 9,5,3,7
3,7,5,9 5,7,9,3 7,9,5,3 9,5,7,3
4. Antiguamente los barcos se comunicaban entre si usando banderas de diferentes colores de manera ordenada.
P4=4!
4*3*2*1= 24 mensajes
P5=5!
5*4*3*2*1=120 mensajes
Permutaciones con repetición
Se llama permutaciones con repetición a los grupos de elementos que se forman cuando "n" elementos,donde e primer elemento se repite n veces, el segundo también se repite n veces y así se repiten hasta llegar al final de la lista. Estas agrupaciones deben seguir las siguientes reglas;
- Entran todos los elementos.
- Si importa el orden.
- Si se repiten los elementos.
La formula para realizar el calculo de las permutaciones con repetición es la siguiente.
PRn=____Pn_____
a! b! c!
Con las cifras 2,2,2,3,3,3,3,4,4 ¿Cuantos números de 9 cifras se pueden formar? Si los datos son n=9 a=3 b=4 c=2
abc
PRn =____Pn______
a! b! c!
3,4,2
PRn =______Pa______= 9*8*7*6*5*4*3*2*1= 9*8*7*6 = 15120 = 1260
3! 4! 2! 3*2*1.4*3+2 *1 6*2 12
Permutaciones Circulares
Las permutaciones circulares se utilizan cuando os elementos se van a ordenar en circulo
Por ejemplo
Los comensales en una mesa se van a sentar de modo que el primer elemento que se situe en la mesa determina el principio y el fin de la lista.
La formula para la permutacion circular es PC n-1=n!
Ejercicio
- De cuantas formas distintas pueden sentarse 8 personas alrededor de una mesa redonda.
PC n-1= n!
PC 8-1= 71 =7*6*5*4*3*2*1= 5040
PERMUTACIONES FORMULA REGLAS
1. Entran todos los elementos.
Permutaciones P4= 4! 2. Si importa el orden.
3. No se repiten los elementos.
Con repetición PRn=__Pn__ 222 3333 44 a! b! c! a b c
Circulares PCn-1 = n! Tienen que ser un problema relacionado a un circulo.
Ejercicios de Permutaciones
- ¿Cuantas palabras distintas de cuatro letras se pueden formar? Escriba el listado que se forma.
Pn = 4!
Pn = n! = 4! = 4*3*2*1= 24 palabras
ALEX LAEX ELAX XAEL
AELX LAXE ELXA XALE
AEXL LXAE EXAL XLAE
AXLE LXEA EXLA XLEA
AXEL LEAX EALX XELA
ALXE LAEX EAXL XEAL
2.¿Cuantas palabras diferentes de 5 letras se puede fomar con la palabra LIBRO?
Pn = n! =5! = 5*4*3*2*1= 120 palabras
3.¿Cuantas palabras diferentes de 6 letras se puede formar la palabra TRATAR?
PRn = ____Pn_____
a! b! c!
2,2,2
PR =____P6_____ = 6*5*4*3*2*1 =___360___ = 90 palabras
2! 2! 2! 2*1 * 2*1 * 2*1 4
4.¿Cuantas palabras de 10 letras se puede formar usando la palabra TERMÓMETRO?
PR =____P10____ = 10*9*8*7*6*5*4*3*2*1 = 1814400 = 113400 palabras
2! 2! 2! 2! 2! 2*1 x 2*1 x 2*1 x 2*1 x 2*1 16
Principios Fundamentales del Conteo
La enumeración o conteo puede parecer un proceso obvio que un estudiante aprende al estudio aritmética por primera vez. Pero luego según parece se presta poca atención en lo que se refiere a un desarrollo mas amplio del conteo, conforme el estudiante pasa áreas mas difíciles de las matemáticas como el álgebra, la geometría, la trigonometria y el calculo. En consecuencia deberá servir como advertencia acerca del conteo.
La enumeración no termina con la aritmética, también tiene aplicaciones como: la teoría de códigos, la probabilidad y la estadística.
Reglas de la Suma y Producto
- Si una primera tarea puede realizarse de "m" formas mientras que una segunda tarea puede realizarse de "n" formas, y no es posible realizar ambas tareas de manera simultanea entonces para llevar a cabo cualquiera de ellas.
- Si un procedimiento se puede descomponer en las etapas primera y segunda, si existe "m" resultados posibles de la primera etapa, para cada uno de estos resultados existen "n" resultados posibles para la segunda etapa, entonces el procedimiento total se puede realizar en el orden dado.
domingo, 7 de abril de 2019
Teoría de Conjuntos
1°- ¿Que es conjunto?
Un conjunto es una colección de elementos con características similares considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser las siguientes: personas, números, colores, letras, figuras, etc. Se dice que un elemento (o miembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.
Ejemplo: el conjunto de los colores del arcoíris es:
- AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}
Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para los números naturales, si se considera la propiedad de ser un número primo, el conjunto de los números primos es:
- P = {2, 3, 5, 7, 11, 13, ...}
-
- 2°-¿Que es conjunto?
- Un conjunto se define como la agrupación de diferentes elementos que comparten entre sí características y propiedades semejantes. Estos elementos pueden ser cualquier cosa, tales como números, canciones, meses, personas, etcétera.A su vez un conjunto puede convertirse también en un elemento.
- Por ejemplo, un ramo de flores. En principio una flor sería el primer elemento, pero al conjunto de flores se lo puede considerar luego como un ramo de flores, convirtiéndose así, en un nuevo elemento.
- 3°-¿Que es un conjunto?
- Lo primero que debemos saber es qué es un conjunto. Podemos definirlo como una colección de objetos, a los que llamamos elementos, que tienen alguna característica común.
Los conjuntos pueden tener elementos de cualquier tipo: números, letras, objetos, personas… Por ejemplo, este conjunto contiene frutas: SUBCONJUNTOS
- 1°-¿Que es un subconjunto?
- Conjunto de elementos que tienen las mismas características y que está incluido dentro de otro conjunto más amplio.
El conjunto de los números pares es un subconjunto del conjunto de los números enteros - 2°-¿Que es un subconjunto?
- Recuerde que un conjunto es una colección de elementos.
Un conjunto A es un subconjunto de un conjunto B si cada elemento en A está también en B .
Por ejemplo, si A = {1, 3, 5} y B = {1, 2, 3, 4, 5}, entonces A es un subconjunto de B , y escribimos
La línea debajo de la U de lado significa que A también puede ser igual a B (esto es, estos pueden ser conjuntos idénticos). Si queremos decir que A es un subconjunto apropiado de B (esto quiere decir: es un subconjunto, pero hay por lo menos un elemento en B que no está en A ) entonces podemos eliminar la línea:
Para escribir que un conjunto no es un subconjunto de otro conjunto, solo coloque una diagonal a través de la U de lado:
- 3°-¿Que es un subconjunto?
- Un subconjunto A de un conjunto B, es un conjunto que contiene algunos de los elementos de B (o quizá todos)
Cuando A es un subconjunto de B, se denota como A ⊆ B y se dice que «A está contenido en B». También puede escribirse B ⊇ A, y decirse queB es un superconjunto de A y también «B contiene a A» o «B incluye aA».Todo conjunto A es un subconjunto de sí mismo, ya que siempre se cumple que «cada elemento de A es a su vez un elemento de A».Es habitual establecer una distinción más fina mediante el concepto de subconjunto propio: A es un subconjunto propio de B si es un subconjunto de B pero no es igual a B. Se denota como A ⊊ B, es decir: A ⊆ B pero A ≠ B (y equivalentemente, para un superconjunto propio, B ⊋ A). -
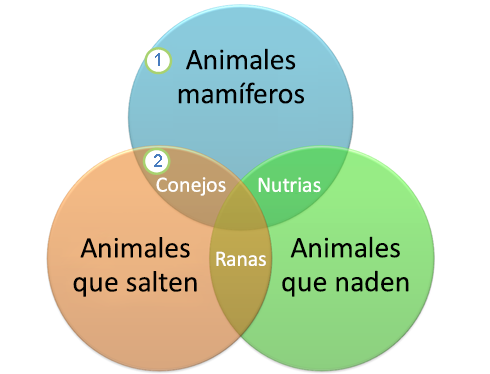
- DIAGRAMAS DE VENN
- Definición 1:
- Un diagrama de Venn usa círculos que se superponen u otras figuras para ilustrar las relaciones lógicas entre dos o más conjuntos de elementos. A menudo, se utilizan para organizar cosas de forma gráfica, destacando en qué se parecen y difieren los elementos. Los diagramas de Venn, también denominados "diagramas de conjunto" o "diagramas lógicos", se usan amplia mente en las áreas de matemática, estadística, lógica, enseñanza, lingüística, informática y negocios.
-
- Definición 2:
- Los diagramas de Venn son esquemas usados en la teoría de conjuntos, tema de interés en matemáticas, lógica de clases y razonamiento diagramático. Estos diagramas muestran colecciones (conjuntos) de cosas (elementos) por medio de líneas cerradas. La línea cerrada exterior abarca a todos los elementos bajo consideración, el conjunto universal U.Los diagramas de Venn fueron ideados hacia 1880 por John Venn.
- Ejemplo 1
- Ejemplo 2
- Ejemplo 3
-
Actividad:Definir las siguientes operaciones y leyes de conjuntos.- Unión: En la teoría de conjuntos, la unión de dos (o más) conjuntos es una operación que resulta en otro conjunto, cuyos elementos son los mismos de los conjuntos iniciales. Por ejemplo, el conjunto de los números naturales es la unión del conjunto de los números pares positivos P y el conjunto de los números impares positivos I:
- ¬ es el operador de negación (NO)
es el operador de conjunción (Y)
es el operador de disyunción (O)
- ⇔ es un símbolo metalógico que significa "puede ser reemplazado en una prueba lógica"
En ambos casos los resultados son iguales. Esta propiedad, particularizada para la suma y el producto, se puede generalizar a cualquier otro par de operaciones aritméticas, obteniendo de esta forma la definición de distributidad.
La negación de la disyunción es la conjunción de las negaciones.
y también,
La unión de conjuntos se denota por el símbolo ∪, de modo que por ejemplo, N = P ∪ I. - Intersección: En teoría de conjuntos, la intersección de dos (o más) conjuntos es una operación que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. Por ejemplo, dado el conjunto de los números pares P y el conjunto de los cuadrados C de números naturales, su intersección es el conjunto de los cuadrados pares D:En otras palabras: Así, por ejemplo, si A = { a, b, c, d, e, f} y B = { a, e, i, o, u}, entonces la intersección de dichos conjuntos estará formada por todos los elementos que estén a la vez en los dos conjuntos, esto es: A∩B = { a, e}La intersección de conjuntos se denota por el símbolo ∩ por lo que D = P ∩ C.
- Complemento: El complemento de un conjunto o conjunto complementario es otro conjunto que contiene todos los elementos que no están en el conjunto original. Para poder definirlo es necesario especificar qué tipo de elementos se están utilizando, o de otro modo, cuál es el conjunto universal. Por ejemplo, si se habla de números naturales, el complementario del conjunto de los números primos P es el conjunto de los números no primos C, que está formado por los números compuestos y el 1:A su vez, el conjunto C es el complementario de P. El conjunto complementario se denota por una barra horizontal o por el superíndice «∁», por lo que se tiene: P∁ = C, y también C = P.El conjunto complementario de A es la diferencia (o complementario relativo) entre el conjunto universal y A, por lo que ambas operaciones (complementario y diferencia) tienen propiedades similares.
- Ley Distributiva: En matemáticas y en particular en álgebra abstracta, la distributiva es la propiedad de los operadores binarios que generaliza la propiedad distributiva del álgebra elemental.La propiedad distributiva de la multiplicación sobre la suma en álgebra elemental es aquella en la que el resultado de un número multiplicado por la suma de dos o más sumando, es igual a la suma de los productos de cada uno sumando por ese número. En términos algebraicos:Ejemplo:
- Ley de Morgan: En lógica proposicional y álgebra de Boole, las leyes de De Morgan son un par de reglas de transformación que son ambas reglas de inferencia válidas. Las normas permiten la expresión de las conjunciones y disyunciones puramente en términos de vía negación.Las reglas se pueden expresar en español como:La negación de la conjunción es la disyunción de las negaciones.o informalmente como:"no (A y B)" es lo mismo que "(no A) o (no B)""no (A o B)" es lo mismo que "(no A) y (no B)"Las reglas pueden ser expresadas en lenguaje formal con dos proposiciones P y Q, de esta forma:donde:Entre la aplicaciones de las normas se incluyen la simplificación de expresiones lógicas en programas de computación y diseño de circuitos digitales. Las leyes de De Morgan son un ejemplo de concepto más general de dualidad matemática.
- Diferencia Simétrica: En teoría de conjuntos, la diferencia simétrica de dos conjuntos es una operación que resulta en otro conjunto cuyos elementos son aquellos que pertenecen a alguno de los conjuntos iniciales, sin pertenecer a ambos a la vez. Por ejemplo, la diferencia simétrica del conjunto de los números pares P y el conjunto de los cuadrados perfectos C es un conjunto D que contiene los cuadrados impares y los pares no cuadrados:La diferencia simétrica de conjuntos se denota por Δ, por lo que P Δ C = D.
Actividad:Definir la relación que existe entre la teoría de conjuntos, lógica matemática y álgebra booleana.- Entre lógica matemática y teoría de conjuntos comparten leyes lógicas tanto para conjuntos como para lógica proposicional. El álgebra de Boole fue un intento de utilizar las técnicas algebraicas para tratar expresiones de la lógica proposicional.En la actualidad, el álgebra de Boole se aplica de forma generalizada en el ámbito del diseño electrónico.

Suscribirse a:
Comentarios (Atom)